Площ на правоъгълник

Какво е правоъгълник?

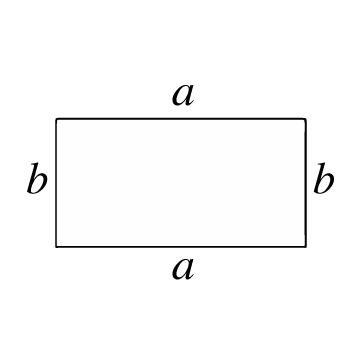
Това е затворен многоъгълник, образуван от 4 страни и 4 върха, при което всеки вътрешен ъгъл е прав (90°). Срещуположните страни са успоредни и с еднаква дължина. Правоъгълникът е подобен на квадрат, с тази разлика, че двете двойки успоредни страни имат различни дължини.

Как да изчислим площта на правоъгълник

Площта на правоъгълник представлява броя единици повърхност вътре в правоъгълника. За да изчислите тази повърхност, първо трябва да знаете дължината на страните, т.е. дължината на всяка отсечка, свързваща два върха на правоъгълника.

Формула за изчисляване на площта на правоъгълник

Практически пример

Да предположим, че ни искат да изчислим площта на правоъгълник и ни дават стойностите на страните: a = 4 [см] и b = 3 [см]

Заместване на стойностите на страните във формулата за площ

Ако вече имаме дължините на страните, образуващи правоъгълника, за да изчислим площта остава само да заместим тези стойности във формулата за площта на правоъгълника. Така получаваме:

Изчисляване на площта на правоъгълник от диагонала и дължината на една от страните

Възможно е в условието на задачата да ни дадат само дължината на диагонала и дължината на една от страните на правоъгълника (известна страна). В тези случаи можем да използваме Питагоровата теорема за определяне на стойността на неизвестната страна и да приложим формулата за изчисляване на площта на правоъгълника, спомената по-горе.

Формула на Питагоровата теорема, приложена към правоъгълник

Тъй като в условието ни дават дължината на диагонала и дължината на една от страните, можем да получим следното уравнение:

Като изразим „неизвестната страна" от уравнението, получаваме следната зависимост:

Тази зависимост е в сила за всички правоъгълници и ще ви позволи да получите дължината на неизвестната страна. След като намерите тази стойност, можете без проблем да приложите формулата за изчисляване на площта на правоъгълника, спомената в жълтия правоъгълник в началото на тази статия.