Площадь прямоугольника
Введите длину сторон прямоугольника, чтобы рассчитать его площадь или поверхность. Используйте точку в качестве десятичного разделителя.
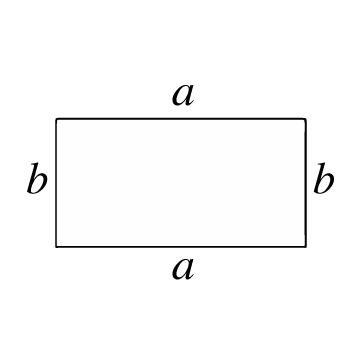
Площадь прямоугольника равна:
Что такое прямоугольник?
Это замкнутый многоугольник, образованный 4 сторонами и 4 вершинами, где каждый внутренний угол является прямым (90°). Противоположные стороны также параллельны и имеют одинаковую длину. Прямоугольник похож на квадрат, за исключением того, что 2 пары параллельных сторон имеют различные длины.
Как рассчитать площадь прямоугольника
Площадь прямоугольника представляет собой количество единиц поверхности, содержащихся внутри прямоугольника. Для расчёта этой площади сначала нужно знать длину его сторон, то есть длину каждого отрезка, соединяющего две вершины прямоугольника.
Формула для расчёта площади прямоугольника
Практический пример
Допустим, нам нужно найти площадь прямоугольника, и нам даны значения его сторон: a = 4 [см] и b = 3 [см].
Подстановка значений сторон в формулу площади
Если мы уже знаем длины сторон прямоугольника, для расчёта площади остаётся только подставить эти значения в формулу площади прямоугольника. Таким образом, получим:
Площадь прямоугольника = (4) · (3)
Площадь прямоугольника = 12 [см²]
Нахождение площади прямоугольника по его диагонали и длине одной из сторон
Возможно, что в условии задачи нам дадут только длину диагонали и длину одной из сторон прямоугольника (известная сторона). В таких случаях можно использовать теорему Пифагора для определения значения недостающей стороны (неизвестная сторона) и применить формулу расчёта площади прямоугольника, указанную выше.
Формула теоремы Пифагора, применённая к прямоугольнику
Диагональ² = (сторона a)² + (сторона b)²
Так как в условии задачи нам даны длина диагонали и длина одной из сторон, мы можем получить следующее уравнение:
Выразив «неизвестную сторону» из уравнения, получим следующее соотношение:
Это соотношение справедливо для всех прямоугольников и позволит вам найти длину недостающей стороны. Определив это значение, вы сможете без проблем применить формулу для расчёта площади прямоугольника, указанную в жёлтой рамке в начале этой статьи.