Площадь квадрата

Что такое квадрат?

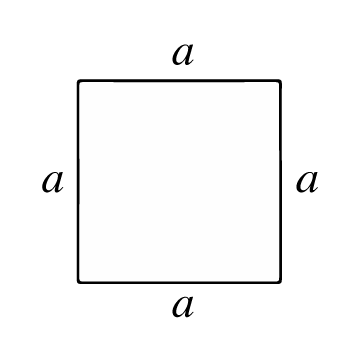
Квадрат — это многоугольник с четырьмя равными сторонами (рёбрами) и прямыми углами. Все его стороны конгруэнтны (имеют одинаковую длину), а его диагонали также конгруэнтны (имеют одинаковую длину). Точки пересечения называются вершинами, и в них образуются 4 внутренних угла по 90° каждый.

Как рассчитать площадь квадрата

Площадь квадрата представляет собой количество единиц поверхности, содержащихся внутри квадрата. Для расчёта этой площади сначала нужно знать длину его стороны или ребра (a), то есть длину отрезка, соединяющего две вершины квадрата.

Формула для расчёта площади квадрата:

Практический пример

Допустим, нам нужно найти площадь квадрата, и нам дано значение его стороны (a), которое в данном примере равно 4 [см].

Подстановка значения стороны в формулу площади

Если мы уже знаем длину стороны (4 см), остаётся только подставить это значение в формулу для расчёта площади квадрата. Таким образом:

Нахождение площади квадрата по его диагонали

Возможно, что в условии задачи единственным данным будет длина диагонали квадрата. В таких случаях можно использовать теорему Пифагора для определения значения стороны квадрата, если учесть, что диагональ является гипотенузой равнобедренного треугольника с внутренними углами 45°, 45° и 90° соответственно.

Формула теоремы Пифагора

По определению все стороны или рёбра квадрата равны. Следовательно, для любого треугольника, образованного диагональю квадрата, основание и высота будут равны. Если мы примем диагональ за гипотенузу, формулу Пифагора можно записать следующим образом:

Выразив сторону из уравнения, получим следующее соотношение:

Это соотношение справедливо для всех квадратов и позволит вам легко найти длину стороны с помощью любого калькулятора. Зная значение стороны, вы можете подставить его в формулу для расчёта площади квадрата, указанную выше в жёлтой рамке.

Как рассчитать площадь квадрата по его периметру

Рассчитать площадь квадрата по его периметру очень просто, поскольку по определению квадрат имеет 4 стороны (ребра) одинакового размера. Зная это, можно сделать вывод, что сторона квадрата равна его периметру, делённому на 4.

Подставляя в формулу площади квадрата, получим:

Практический пример

Допустим, нам нужно найти площадь квадрата с периметром 24 [см]. Подставляя значение периметра в формулу площади, получим: