مساحة المستطيل

ما هو المستطيل؟

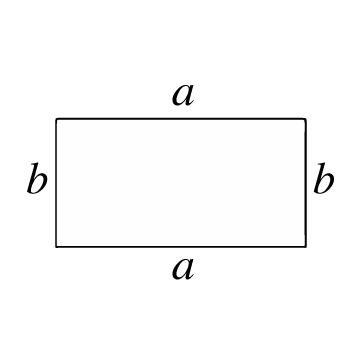
هو مضلع مغلق يتكوّن من 4 أضلاع و4 رؤوس، حيث تشكّل كل زاوية داخلية زاوية قائمة (90°). الأضلاع المتقابلة متوازية ومتساوية في الطول. يشبه المستطيل المربع، إلا أن زوجي الأضلاع المتوازية لهما أطوال مختلفة.

كيفية حساب مساحة المستطيل

تمثّل مساحة المستطيل عدد وحدات المساحة الموجودة داخله. لحساب هذه المساحة، يجب أولاً معرفة أطوال أضلاعه، أي طول كل قطعة مستقيمة تصل بين رأسين من رؤوس المستطيل.

صيغة حساب مساحة المستطيل

مثال عملي

لنفترض أنه طُلب منا حساب مساحة مستطيل وأُعطينا قيم أضلاعه، حيث a = 4 [سم] وb = 3 [سم]

التعويض بقيم الأضلاع في صيغة المساحة

إذا كنا نعرف أطوال أضلاع المستطيل، فلحساب المساحة ما تبقى سوى التعويض بهذه القيم في صيغة مساحة المستطيل. وبذلك نحصل على:

حساب مساحة المستطيل من قطره وطول أحد أضلاعه

من الممكن أن يُعطى في نص المسألة فقط طول القطر وطول أحد أضلاع المستطيل (الضلع المعلوم). في هذه الحالة، يمكن استخدام نظرية فيثاغورس لتحديد قيمة الضلع المجهول وتطبيق صيغة حساب مساحة المستطيل المذكورة أعلاه.

صيغة نظرية فيثاغورس مطبّقة على المستطيل

بما أن نص المسألة يعطينا طول القطر وطول أحد الأضلاع، يمكننا الحصول على المعادلة التالية:

بحل المعادلة بالنسبة للضلع المجهول، نحصل على العلاقة التالية:

تنطبق هذه العلاقة على جميع المستطيلات وتتيح لك الحصول على طول الضلع المجهول. بمجرد إيجاد هذه القيمة، يمكنك تطبيق صيغة حساب مساحة المستطيل المذكورة في المربع الأصفر في بداية هذا المقال.