Площа квадрата

Що таке квадрат?

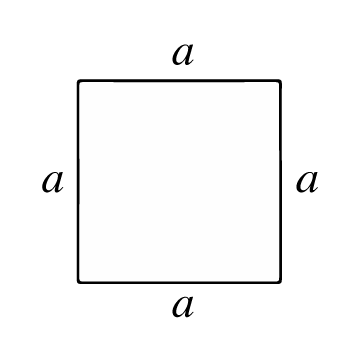
Квадрат — це багатокутник з чотирма рівними сторонами (ребрами) та прямими кутами. Усі його сторони конгруентні (мають однакову довжину), а його діагоналі також конгруентні (також мають однакову довжину). Точки перетину називаються вершинами, і від них утворюються 4 внутрішніх кути по 90° кожен.

Як розрахувати площу квадрата

Площа квадрата — це кількість одиниць поверхні, що міститься всередині квадрата. Для обчислення цієї поверхні спочатку потрібно знати довжину його сторони або ребра (a), тобто довжину відрізка, що з'єднує дві вершини квадрата.

Формула для обчислення площі квадрата:

Практичний приклад

Припустимо, що нас просять знайти площу квадрата і надають значення його сторони (a), яка для цього прикладу дорівнює 4 [см].

Підставляємо значення сторони у формулу площі

Якщо ми вже знаємо довжину сторони (4 см), то залишається лише підставити це значення у формулу для обчислення площі квадрата. Отже:

Обчислення площі квадрата за його діагоналлю

Можливо, що в умові задачі єдиним відомим значенням є довжина діагоналі квадрата. У таких випадках можна використати теорему Піфагора для визначення значення сторони квадрата, якщо врахувати, що діагональ є гіпотенузою рівнобедреного трикутника з внутрішніми кутами 45°, 45° та 90° відповідно.

Формула теореми Піфагора

За визначенням, усі сторони або ребра квадрата рівні. Тому справедливо припустити, що для будь-якого трикутника, утвореного діагоналлю квадрата, основа та висота будуть рівними. Якщо вважати діагональ гіпотенузою, формулу Піфагора можна переписати так:

Виразивши сторону з рівняння, отримаємо таке співвідношення:

Це співвідношення справедливе для всіх квадратів і дозволить вам отримати довжину сторони простим способом за допомогою будь-якого калькулятора. Знаючи значення сторони, ви можете підставити його у формулу для обчислення площі квадрата, наведену вище у жовтій рамці.

Як розрахувати площу квадрата за його периметром

Розрахувати площу квадрата за його периметром дуже просто, адже за визначенням квадрат має 4 сторони (ребра) однакового розміру. З огляду на це, можна зробити висновок, що сторона квадрата дорівнює його периметру, поділеному на 4.

Підставляючи у формулу площі квадрата, отримуємо:

Практичний приклад

Припустимо, що нас просять знайти площу квадрата з периметром 24 [см]. Підставляючи значення периметра у формулу площі, отримуємо: