Vierkant Oppervlakte

Wat is een vierkant?

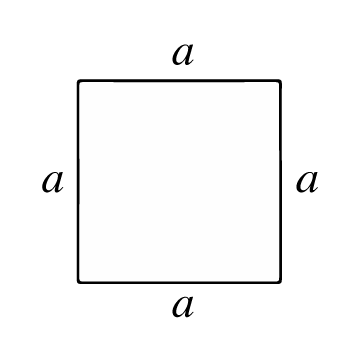
Een vierkant is een veelhoek met vier gelijke zijden en rechte hoeken. Alle zijden zijn congruent (hebben dezelfde lengte) en de diagonalen zijn congruent (hebben ook dezelfde lengte). De snijpunten worden hoeken genoemd, en vanaf deze worden vier interne hoeken van 90° gevormd.

Hoe het oppervlak van een vierkant te berekenen

Het oppervlak van een vierkant vertegenwoordigt het aantal oppervlakte-eenheden binnen het vierkant. Om dit oppervlak te berekenen, moet je eerst de lengte van de zijde (a) weten, dat wil zeggen de lengte van de lijn die twee hoeken van het vierkant verbindt.

Formule om het oppervlak van een vierkant te berekenen:

Praktisch voorbeeld

Stel dat we het oppervlak van een vierkant moeten vinden en we de waarde van de zijde (a) hebben, die in dit voorbeeld 4 [cm] is.

Vervang de waarde van de zijde in de oppervlakformule

Als we de lengte van de zijde (4 cm) al hebben, moeten we alleen deze waarde vervangen in de formule om het oppervlak van het vierkant te berekenen. Het resultaat is:

Bereken het vierkant oppervlak uit de diagonaal

Het is mogelijk dat in een probleem je alleen de lengte van de diagonaal van een vierkant hebt. In dit geval kun je de stelling van Pythagoras gebruiken om de lengte van de zijde van het vierkant te bepalen, als je ervan uitgaat dat de diagonaal de hypotenusa is van een rechthoekige driehoek met interne hoeken van 45°, 45° en 90°.

Pythagoras-formule

Volgens de definitie zijn alle zijden of randen van een vierkant gelijk. Het is redelijk om aan te nemen dat voor elke driehoek die wordt gevormd door de diagonaal van het vierkant, de basis en de hoogte gelijk zijn. Als we de diagonaal als de hypotenusa beschouwen, kunnen we de stelling van Pythagoras als volgt herschrijven:

Door voor de zijde op te lossen in de formule, krijgen we de volgende relatie:

Deze relatie geldt voor alle vierkanten en stelt je in staat om de zijde eenvoudig te berekenen met een rekenmachine. Zodra je de zijde weet, kun je deze vervangen in de formule om het oppervlak van het vierkant te berekenen, zoals vermeld in de gele doos hierboven.

Hoe het vierkantoppervlak te berekenen uit de omtrek

Het berekenen van het oppervlak van een vierkant vanuit de omtrek is heel eenvoudig, aangezien een vierkant per definitie 4 gelijke zijden (a-randen) heeft. Met deze achtergrond kunnen we afleiden dat de zijde van een vierkant gelijk is aan de omtrek gedeeld door 4.

Door de formule voor het vierkantoppervlak in te vullen, hebben we:

Praktisch voorbeeld

Stel dat we het oppervlak van een vierkant moeten vinden met een omtrek van 24 [cm]. Als we de waarde van de omtrek in de formule vervangen, krijgen we: