Oppervlakte van een rechthoek
Voer de lengtes van de zijden van de rechthoek in om de oppervlakte te berekenen. Gebruik een punt als decimaalteken.
De oppervlakte van de rechthoek is:
Wat is een rechthoek?
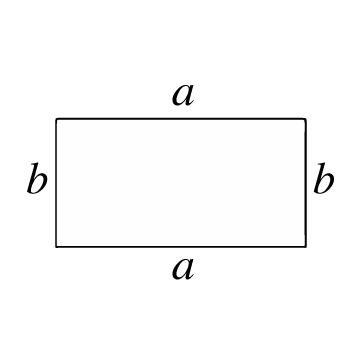
Het is een gesloten veelhoek, gevormd door 4 zijden en 4 hoeken, waarbij elke interne hoek een rechte hoek (90°) vormt. De tegenovergestelde zijden zijn ook parallel en van dezelfde lengte. Een rechthoek lijkt op een vierkant, behalve dat de 2 paren parallelle zijden verschillende lengtes hebben.
Hoe bereken je de oppervlakte van een rechthoek?
De oppervlakte van een rechthoek vertegenwoordigt het aantal vierkante eenheden binnenin de rechthoek. Om deze oppervlakte te berekenen, moet je de lengtes van de zijden weten, dat wil zeggen de lengtes van elke lijn die twee hoeken van de rechthoek verbindt.
Formule om de oppervlakte van een rechthoek te berekenen
Praktisch voorbeeld
Stel dat we de oppervlakte van een rechthoek moeten berekenen, en we hebben de waarden van de zijden, met a = 4 [cm] en b = 3 [cm].
De waarden van de zijden in de oppervlakteformule vervangen
Als we al de lengtes van de zijden hebben die de rechthoek vormen, is het berekenen van de oppervlakte zo eenvoudig als deze waarden in de oppervlakteformule voor een rechthoek in te vullen. We hebben dan:
Oppervlakte van de rechthoek = (4) × (3)
Oppervlakte van de rechthoek = 12 [cm²]
Bereken de oppervlakte van een rechthoek op basis van de diagonaal en de lengte van een van de zijden
Het kan zijn dat we in een probleem alleen de lengte van de diagonaal en de lengte van een van de zijden van de rechthoek (de bekende zijde) hebben. In dat geval kunnen we de stelling van Pythagoras gebruiken om de waarde van de ontbrekende zijde te bepalen en de oppervlakteformule voor de rechthoek die hierboven is genoemd toe te passen.
De stelling van Pythagoras toegepast op een rechthoek
Diagonaal² = (zijde a)² + (zijde b)²
Omdat de opgave ons de lengte van de diagonaal en de lengte van een van de zijden geeft, kunnen we de volgende vergelijking verkrijgen:
Door de "ontbrekende zijde" in de vergelijking om te vormen, krijgen we de volgende relatie:
Deze relatie geldt voor alle rechthoeken en zal je in staat stellen de lengte van de zijde te vinden die je nodig hebt. Zodra je deze waarde hebt gevonden, kun je de oppervlakteformule voor een rechthoek probleemloos toepassen, zoals vermeld in het gele vak aan het begin van dit artikel.