球の面積

球とは？

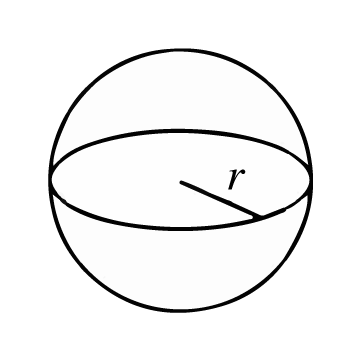
球は、すべての点が中心と呼ばれる内部の一点から等距離にある曲面で構成される三次元の幾何学図形です。曲面と中心の間の距離を半径と呼びます。

球の面積の求め方

球の面積は、球の表面（「殻」）にある面積の単位数を表します。この表面積を計算するには、まず半径 (r) の長さ、つまり球の中心点から表面上の任意の点までの距離を知る必要があります。与えられた情報が直径の場合、直径 (d) の長さを2で割るだけで半径を求めることができます。

球の面積を計算する公式：

実践例

球の面積を求めるよう求められ、少し複雑にするために直径の長さが与えられたとしましょう。この例では、直径の長さを10 [cm] とします。

ステップ1：半径 (r) の長さを求める

球の直径 (d) がわかっている場合、それを2で割ると半径 (r) が得られます。この例では：

問題文で半径が直接与えられている場合は、このステップを省略してステップ2に進むことができます。

ステップ2：求めた半径を面積の公式に代入する

前のステップで、この例では半径 = 5 [cm] が得られました。あとはこの長さを球の面積の公式に代入するだけです。

以上です。とても簡単に球の面積（表面積）を計算することができました。直径と半径の関係を覚えておくことが、このような数学の問題を解く上で重要です。