長方形の面積
長方形の辺の長さを入力して面積を計算します。小数点にはピリオドを使用してください。
辺 (a) が無効です。
辺 (b) が無効です。
長方形の面積は:
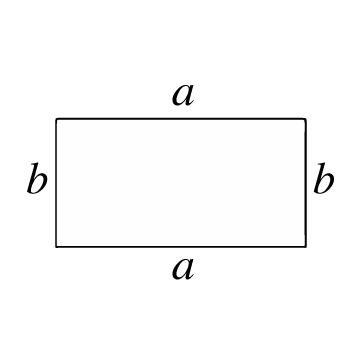
長方形とは?
4つの辺と4つの頂点からなる閉じた多角形で、各内角は直角(90°)を形成します。対辺は平行で同じ長さです。長方形は正方形に似ていますが、2組の平行な辺の長さが異なります。
長方形の面積の計算方法
長方形の面積は、長方形の内部にある面積の単位数を表します。この面積を計算するには、まず辺の長さ、つまり長方形の2つの頂点を結ぶ各線分の長さを知る必要があります。
長方形の面積を計算する公式
長方形の面積 = (辺 a) · (辺 b)
実践例
長方形の面積を求めるよう求められ、辺の値が a = 4 [cm]、b = 3 [cm] と与えられたとしましょう。
辺の値を面積の公式に代入する
長方形を構成する辺の長さがわかっているので、面積を計算するにはこれらの値を長方形の面積の公式に代入するだけです。したがって:
長方形の面積 = (辺 a) · (辺 b)
長方形の面積 = (4) · (3)
長方形の面積 = 12 [cm²]
長方形の面積 = (4) · (3)
長方形の面積 = 12 [cm²]
対角線と一辺の長さから長方形の面積を求める
問題文で、長方形の対角線の長さと一辺の長さ(既知の辺)だけが与えられる場合があります。このような場合、ピタゴラスの定理を使って不明な辺(未知の辺)の値を求め、上記の長方形の面積の公式を適用できます。
長方形に適用するピタゴラスの定理の公式
斜辺² = 底辺² + 高さ²
対角線² = (辺 a)² + (辺 b)²
対角線² = (辺 a)² + (辺 b)²
問題文で対角線の長さと一辺の長さが与えられているので、次の方程式が得られます:
対角線² = (既知の辺)² + (未知の辺)²
「未知の辺」について解くと、次の関係が得られます:
未知の辺 = √(対角線² - 既知の辺²)
この関係はすべての長方形に当てはまり、不明な辺の長さを求めることができます。この値がわかったら、この記事の冒頭の黄色い枠で説明した長方形の面積の公式を問題なく適用できます。