Surface d'une Sphère

Qu'est-ce qu'une Sphère?

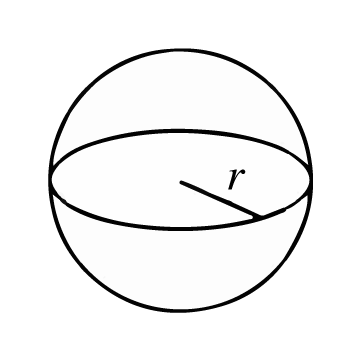
C'est une figure géométrique tridimensionnelle composée d'une surface courbe dont les points sont tous à égale distance d'un point intérieur appelé centre. La distance entre la surface courbe et le centre est appelée le rayon.

Comment calculer la surface d'une sphère

La surface d'une sphère représente le nombre d'unités de surface que possède la peau ou la "coque" d'une sphère. Pour calculer cette surface, vous devez d'abord connaître la longueur de son rayon (r), c'est-à-dire la distance du centre de la sphère à n'importe quel point de la peau ou de la surface. Si l'information que vous avez est le diamètre, vous pouvez obtenir le rayon en divisant simplement la longueur du diamètre (d) par 2.

Formule pour calculer la surface d'une sphère:

Exemple pratique

Disons que l'on vous demande de calculer la surface d'une sphère et que l'on vous donne la longueur de son diamètre, pour ajouter un peu de complexité. Pour cet exemple, la longueur du diamètre est de 10 [cm].

Étape 1 : Déterminer la longueur du rayon (r)

Si vous connaissez déjà le diamètre (d) de la sphère, vous le divisez par 2 et obtenez le rayon (r). Pour cet exemple, nous avons donc :

Si dans l'énoncé de l'exercice, on vous donne directement le rayon, vous pouvez sauter cette étape et passer directement à l'étape 2.

Étape 2 : Remplacer le rayon obtenu dans la formule de la surface

De l'étape précédente, nous avons obtenu la valeur du rayon = 5 [cm] pour cet exemple. Il nous suffit maintenant de remplacer cette longueur dans la formule pour calculer la surface de la sphère.

Et voilà. Nous avons calculé très simplement la surface d'une sphère. Il est important de se rappeler de la relation entre le diamètre et le rayon pour résoudre tout exercice mathématique de ce type.