Superficie d'un Rectangle
Saisissez la longueur des côtés du rectangle pour calculer sa superficie. Utilisez le point comme séparateur décimal.
La superficie du rectangle est :
Qu'est-ce qu'un rectangle?
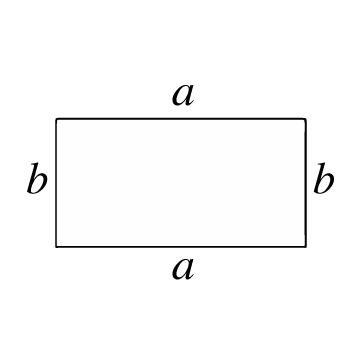
C'est un polygone fermé composé de 4 côtés et 4 sommets, où chaque angle intérieur forme un angle droit (90°). Les côtés opposés ont également la particularité d'être parallèles et de même longueur. Un rectangle est similaire à un carré, à la différence que les deux paires de côtés parallèles ont des longueurs différentes.
Comment calculer la superficie d'un rectangle
La superficie d'un rectangle représente le nombre d'unités de superficie que possède un rectangle à l'intérieur. Pour calculer cette superficie, vous devez d'abord connaître la longueur de ses côtés, c'est-à-dire la longueur de chaque trait qui relie deux sommets du rectangle.
Formule pour calculer la superficie d'un rectangle
Exemple pratique
Supposons que l'on vous demande de calculer la superficie d'un rectangle et que l'on vous donne les valeurs de ses côtés, avec a = 4 [cm] et b = 3 [cm].
Remplacement des valeurs des côtés dans la formule de la superficie
Si vous avez déjà la longueur des côtés qui composent le rectangle, pour calculer la superficie, il vous suffit de remplacer ces valeurs dans la formule de la superficie du rectangle. De cette manière, nous avons :
Superficie rectangle = (4) · (3)
Superficie rectangle = 12 [cm²]
Calcul de la superficie d'un rectangle à partir de sa diagonale et de la longueur de l'un de ses côtés
Il se peut que dans l'énoncé d'un exercice, on vous donne uniquement la longueur de la diagonale et la longueur de l'un des côtés du rectangle (côté connu). Dans ce cas, vous pouvez utiliser le théorème de Pythagore pour déterminer la valeur du côté que vous ne connaissez pas (côté manquant) et appliquer la formule pour calculer la superficie du rectangle mentionnée au début de cet article.
Formule du théorème de Pythagore appliquée à un rectangle
Diagonale² = (côté a)² + (côté b)²
Comme l'énoncé de l'exercice vous donne la longueur de la diagonale et la longueur de l'un de ses côtés, vous pouvez obtenir l'équation suivante :
En résolvant pour le "côté manquant" de l'équation, vous obtiendrez la relation suivante :
Cette relation est valable pour tous les rectangles et vous permettra d'obtenir la longueur du côté que vous ne connaissez pas. Une fois que vous avez trouvé cette valeur, vous pouvez facilement appliquer la formule pour calculer la superficie du rectangle mentionnée dans le cadre jaune au début de cet article.