Plocha čtverce

Co je čtverec?

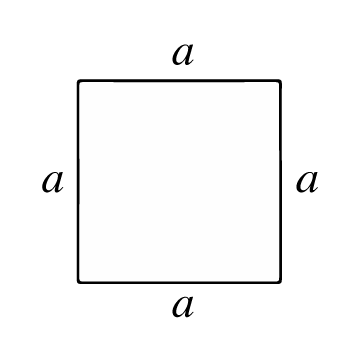
Čtverec je mnohoúhelník se čtyřmi stejnými stranami a pravými úhly. Všechny jeho strany jsou kongruentní (mají stejnou délku) a jeho diagonály jsou kongruentní (také mají stejnou délku). Místa, kde se strany protínají, se nazývají vrcholy, a z nich vznikají čtyři vnitřní úhly 90°.

Jak vypočítat plochu čtverce

Plocha čtverce představuje počet povrchových jednotek uvnitř čtverce. Pro výpočet této plochy musíte nejprve znát délku jeho strany (a), tedy délku linie spojující dva vrcholy čtverce.

Vzorec pro výpočet plochy čtverce:

Praktický příklad

Představme si, že musíme najít plochu čtverce, a máme hodnotu jeho strany (a), která v tomto příkladu bude 4 [cm].

Nahrazení hodnoty strany ve vzorci pro plochu

Pokud již máme délku strany (4 cm), zbývá pouze tuto hodnotu dosadit do vzorce pro výpočet plochy čtverce. Výsledek bude:

Výpočet plochy čtverce z jeho diagonály

Může se stát, že v zadání úkolu máte pouze délku nebo velikost diagonály čtverce. V těchto případech můžete použít Pythagorovu větu k určení hodnoty strany čtverce, pokud předpokládáte, že diagonála je úhlopříčkou rovnostranného trojúhelníka s vnitřními úhly 45°, 45° a 90°.

Pythagorův vzorec

Podle definice jsou všechny strany nebo hrany čtverce stejné. Je možné předpokládat, že pro každý trojúhelník vytvořený diagonálou čtverce bude základna a výška stejné. Pokud považujeme diagonálu za přeponu, můžeme Pythagorův vzorec přepsat takto:

Po vyřešení pro stranu v rovnici získáme následující vztah:

Tento vztah platí pro všechny čtverce a umožňuje vám najít délku strany jednoduše pomocí jakékoliv kalkulačky. Jakmile znáte délku strany, můžete ji dosadit do vzorce pro výpočet plochy čtverce uvedeného v žlutém rámečku výše.

Jak vypočítat plochu čtverce z jeho obvodu

Výpočet plochy čtverce z jeho obvodu je velmi jednoduchý, protože podle definice má čtverec 4 strany (a hrany) stejné velikosti. S tímto pozadím můžeme odvodit, že strana čtverce je ekvivalentní jeho obvodu dělenému 4.

Po dosazení do vzorce pro plochu čtverce máme:

Praktický příklad

Představme si, že musíme najít plochu čtverce s obvodem 24 [cm]. Po dosazení hodnoty obvodu do vzorce pro plochu máme: