مستطیل کا رقبہ

مستطیل کیا ہے؟

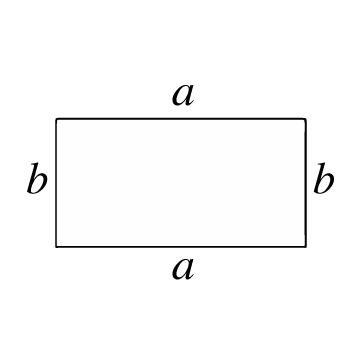
یہ ایک بند کثیرالاضلاع ہے جو 4 اضلاع اور 4 رؤوس پر مشتمل ہے، جہاں ہر اندرونی زاویہ قائمہ (90°) بناتا ہے۔ مقابل اضلاع متوازی اور یکساں لمبائی کی ہوتی ہیں۔ مستطیل مربع سے ملتا جلتا ہے، سوائے اس کے کہ متوازی اضلاع کے 2 جوڑوں کی لمبائی مختلف ہوتی ہے۔

مستطیل کا رقبہ کیسے معلوم کریں

مستطیل کا رقبہ اس کے اندر سطحی اکائیوں کی تعداد کی نمائندگی کرتا ہے۔ اس سطح کا حساب لگانے کے لیے، پہلے آپ کو اس کی اضلاع کی لمبائی معلوم ہونی چاہیے، یعنی مستطیل کے دو رؤوس کو ملانے والی ہر لکیر کی لمبائی۔

مستطیل کا رقبہ معلوم کرنے کا فارمولا

عملی مثال

فرض کریں کہ ہمیں ایک مستطیل کا رقبہ معلوم کرنا ہے اور ہمیں اس کی اضلاع کی قدریں دی گئی ہیں، جہاں a = 4 [سینٹی میٹر] اور b = 3 [سینٹی میٹر]

اضلاع کی قدریں رقبے کے فارمولے میں رکھیں

اگر ہمارے پاس پہلے سے مستطیل کی اضلاع کی لمبائی ہے، تو رقبہ معلوم کرنے کے لیے ہمیں بس ان قدروں کو مستطیل کے رقبے کے فارمولے میں رکھنا ہے۔ اس طرح:

مستطیل کا رقبہ اس کے قطر اور ایک ضلع کی لمبائی سے معلوم کریں

ممکن ہے کہ کسی سوال میں ہمیں صرف قطر کی لمبائی اور مستطیل کی ایک ضلع (معلوم ضلع) دی جائے۔ ایسی صورت میں، ہم فیثاغورث کا نظریہ استعمال کر کے نامعلوم ضلع کی قدر معلوم کر سکتے ہیں اور اوپر بیان کیے گئے مستطیل کے رقبے کا فارمولا لگا سکتے ہیں۔

مستطیل پر فیثاغورث کے نظریے کا فارمولا

چونکہ سوال میں ہمیں قطر کی لمبائی اور ایک ضلع دی گئی ہے، ہم یہ مساوات حاصل کر سکتے ہیں:

مساوات سے "نامعلوم ضلع" نکالنے پر، ہمیں یہ تعلق ملتا ہے:

یہ تعلق تمام مستطیلوں کے لیے درست ہے اور آپ کو نامعلوم ضلع کی لمبائی معلوم کرنے میں مدد دے گا۔ یہ قدر حاصل کرنے کے بعد، آپ بغیر کسی مسئلے کے اس مضمون کے شروع میں بیان کیے گئے مستطیل کے رقبے کا فارمولا لگا سکتے ہیں۔