مربع کا رقبہ

مربع کیا ہے؟

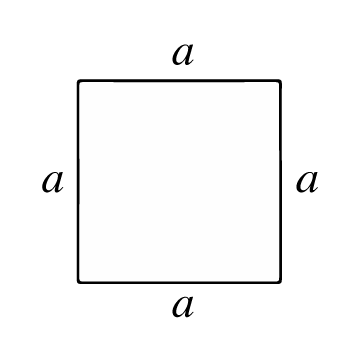
مربع ایک کثیرالاضلاع ہے جس کی چار اضلاع (بازو) برابر اور زاویے قائمہ ہوتے ہیں۔ اس کی تمام اضلاع ہم پیما ہیں (یکساں لمبائی کی ہیں) اور اس کے اقطار بھی ہم پیما ہیں (یکساں لمبائی کے ہیں)۔ تقاطع کے نقاط کو رؤوس کہتے ہیں اور ان سے 4 اندرونی زاویے بنتے ہیں جن میں سے ہر ایک 90 ڈگری کا ہوتا ہے۔

مربع کا رقبہ کیسے معلوم کریں

مربع کا رقبہ اس کے اندر سطحی اکائیوں کی تعداد کی نمائندگی کرتا ہے۔ اس سطح کا حساب لگانے کے لیے، پہلے آپ کو اس کی ضلع یا بازو (a) کی لمبائی معلوم ہونی چاہیے، یعنی مربع کے دو رؤوس کو ملانے والی لکیر کی لمبائی۔

مربع کا رقبہ معلوم کرنے کا فارمولا:

عملی مثال

فرض کریں کہ ہمیں ایک مربع کا رقبہ معلوم کرنا ہے اور ہمیں اس کی ضلع (a) کی قدر دی گئی ہے جو اس مثال میں 4 [سینٹی میٹر] ہے۔

ضلع کی قدر کو رقبے کے فارمولے میں رکھیں

اگر ہمارے پاس پہلے سے ضلع کی لمبائی (4 سینٹی میٹر) ہے، تو ہمیں بس اس قدر کو مربع کے رقبے کے فارمولے میں رکھنا ہے۔ چنانچہ:

مربع کا رقبہ اس کے قطر سے معلوم کریں

ممکن ہے کہ کسی سوال میں آپ کو صرف مربع کے قطر کی لمبائی دی جائے۔ ایسی صورت میں، آپ فیثاغورث کا نظریہ استعمال کر کے مربع کی ضلع کی قدر معلوم کر سکتے ہیں، اگر آپ قطر کو 45°، 45° اور 90° کے اندرونی زاویوں والے متساوی الساقین مثلث کا وتر سمجھیں۔

فیثاغورث کے نظریے کا فارمولا

تعریف کے مطابق، مربع کی تمام اضلاع یا بازو برابر ہوتے ہیں۔ لہٰذا یہ فرض کرنا درست ہے کہ مربع کے قطر سے بننے والے ہر مثلث میں قاعدہ اور عمود برابر ہوں گے۔ اگر ہم قطر کو وتر سمجھیں، تو فیثاغورث کا فارمولا اس طرح لکھا جا سکتا ہے:

مساوات سے ضلع نکالنے پر، ہمیں یہ تعلق ملتا ہے:

یہ تعلق تمام مربعوں کے لیے درست ہے اور آپ کو کسی بھی کیلکولیٹر کی مدد سے آسانی سے ضلع کی لمبائی معلوم کرنے میں مدد دے گا۔ ضلع کی قدر معلوم ہونے کے بعد، آپ اسے اوپر دیے گئے مربع کے رقبے کے فارمولے میں رکھ سکتے ہیں۔

مربع کا رقبہ محیط سے کیسے معلوم کریں

مربع کا رقبہ اس کے محیط سے معلوم کرنا بہت آسان ہے، کیونکہ تعریف کے مطابق مربع کی 4 اضلاع (بازو) یکساں ہوتی ہیں۔ اس بنیاد پر، ہم یہ نتیجہ نکال سکتے ہیں کہ مربع کی ضلع اس کے محیط کو 4 سے تقسیم کرنے کے برابر ہے۔

مربع کے رقبے کے فارمولے میں رکھنے پر:

عملی مثال

فرض کریں کہ ہمیں ایک ایسے مربع کا رقبہ معلوم کرنا ہے جس کا محیط 24 [سینٹی میٹر] ہے۔ محیط کی قدر رقبے کے فارمولے میں رکھنے پر: