Téglalap területe
Add meg a téglalap oldalainak hosszát a terület vagy felület kiszámításához. Használj pontot tizedes elválasztóként.
A téglalap területe:
Mi az a téglalap?
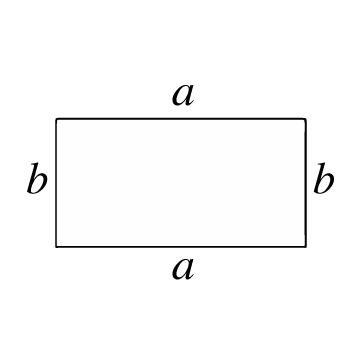
Olyan zárt sokszög, amelyet 4 oldal és 4 csúcs alkot, ahol minden belső szög derékszög (90°). A szemközti oldalak párhuzamosak és egyenlő hosszúak. A téglalap hasonló a négyzethez, azzal a különbséggel, hogy a 2 pár párhuzamos oldal különböző hosszúságú.
Hogyan számítsuk ki a téglalap területét
A téglalap területe a téglalap belsejében lévő felületegységek számát jelenti. A felület kiszámításához először ismerni kell az oldalak hosszát, vagyis a téglalap két csúcsát összekötő szakaszok hosszát.
Képlet a téglalap területének kiszámításához
Gyakorlati példa
Tegyük fel, hogy a téglalap területét kell kiszámolnunk, és megadják az oldalai értékét: a = 4 [cm] és b = 3 [cm]
Az oldalak értékének behelyettesítése a terület képletébe
Ha már ismerjük a téglalapot alkotó oldalak hosszát, a terület kiszámításához csak ezeket az értékeket kell behelyettesíteni a téglalap területének képletébe. Így:
Téglalap területe = (4) · (3)
Téglalap területe = 12 [cm²]
Téglalap területének kiszámítása átlója és az egyik oldala alapján
Lehetséges, hogy a feladat szövegében csak az átló hosszát és a téglalap egyik oldalának hosszát (ismert oldal) adják meg. Ilyen esetekben a Pitagorasz-tételt használhatjuk a hiányzó oldal (ismeretlen oldal) értékének meghatározásához, majd alkalmazhatjuk a fent említett téglalap területének képletét.
Pitagorasz-tétel képlete téglalapra alkalmazva
Átló² = (a oldal)² + (b oldal)²
Mivel a feladat szövegében megadják az átló hosszát és az egyik oldal hosszát, a következő egyenletet kapjuk:
A "hiányzó oldal" kifejezése az egyenletből a következő összefüggést adja:
Ez az összefüggés minden téglalapra érvényes, és lehetővé teszi az ismeretlen oldal hosszának meghatározását. Miután megtaláltuk ezt az értéket, gond nélkül alkalmazhatjuk a cikk elején említett sárga keretben szereplő téglalap területének képletét.