Négyzet területe

Mi az a négyzet?

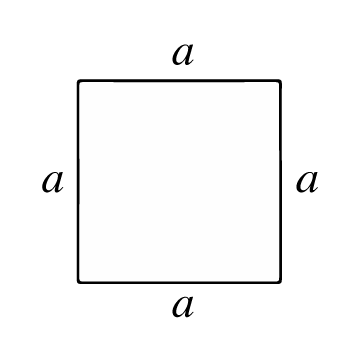
A négyzet egy négyszög, amelynek négy egyenlő éle (oldala) és derékszögei vannak. Minden oldala egybevágó (azonos hosszúságú), és átlói is egybevágóak (szintén azonos hosszúságúak). A metszéspontokat csúcsoknak nevezzük, és ezekből 4 belső szög alakul ki, mindegyik 90°-os.

Hogyan számítsuk ki a négyzet területét

A négyzet területe a négyzet belsejében lévő felületegységek számát jelenti. A felület kiszámításához először ismerni kell az oldal vagy él (a) hosszát, vagyis a négyzet két csúcsát összekötő szakasz hosszát.

Képlet a négyzet területének kiszámításához:

Gyakorlati példa

Tegyük fel, hogy a négyzet területét kell kiszámolnunk, és megadják az él (a) értékét, amely ebben a példában 4 [cm] lesz.

Az él értékének behelyettesítése a terület képletébe

Ha már kiszámoltuk az él hosszát (4 cm), akkor csak ezt az értéket kell behelyettesíteni a négyzet területének kiszámítására szolgáló képletbe. Valóban:

Négyzet területének kiszámítása átlója alapján

Lehetséges, hogy a feladat szövegében az egyetlen adat a négyzet átlójának hossza. Ilyen esetekben a Pitagorasz-tételt használhatod az él értékének meghatározásához, ha úgy tekinted az átlót, mint egy egyenlő szárú háromszög átfogóját, amelynek belső szögei 45°, 45° és 90°.

Pitagorasz-tétel képlete

Definíció szerint a négyzet minden oldala vagy éle egyenlő. Ezért érvényes feltételezni, hogy minden olyan háromszögnél, amelyet a négyzet átlója alkot, az alap és a magasság egyenlő lesz. Ha az átlót tekintjük átfogónak, a Pitagorasz-képletet a következő formában írhatjuk át:

Az él kifejezése az egyenletből a következő összefüggést adja:

Ez az összefüggés minden négyzetre érvényes, és egyszerűen megkaphatod az él hosszát bármilyen számológép használatával. Miután már ismered az él értékét, behelyettesítheted a fenti sárga keretben említett képletbe a négyzet területének kiszámításához.

Hogyan számítsuk ki a négyzet területét kerülete alapján

A négyzet területének kiszámítása kerülete alapján nagyon egyszerű, mivel definíció szerint a négyzetnek 4 egyforma éle (oldala) van. Ezt figyelembe véve arra következtethetünk, hogy a négyzet éle egyenlő a kerületének 4-gyel való osztásával.

Behelyettesítve a négyzet területének képletébe:

Gyakorlati példa

Tegyük fel, hogy egy 24 [cm] kerületű négyzet területét kell kiszámolnunk. A kerület értékének behelyettesítésével a terület képletébe: