Pole prostokąta
Wpisz długość boków prostokąta, aby obliczyć jego pole. Użyj kropki jako separatora dziesiętnego.
Pole prostokąta wynosi:
Co to jest prostokąt?
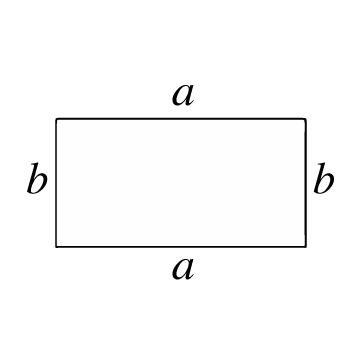
Jest to zamknięty wielokąt, który składa się z 4 boków i 4 wierzchołków, gdzie każdy kąt wewnętrzny tworzy kąt prosty (90°). Przeciwległe boki są również równoległe i mają tę samą długość. Prostokąt przypomina kwadrat, z tym że dwie pary przeciwległych boków mają różne długości.
Jak obliczyć pole prostokąta
Pole prostokąta reprezentuje liczbę jednostek kwadratowych wewnątrz prostokąta. Aby obliczyć to pole, musisz znać długości jego boków, czyli długości każdej linii łączącej dwa wierzchołki prostokąta.
Wzór na pole prostokąta
Przykład praktyczny
Załóżmy, że musimy obliczyć pole prostokąta, a znamy wartości jego boków, gdzie a = 4 [cm] i b = 3 [cm].
Podstawienie wartości boków do wzoru na pole
Jeśli już znamy długości boków tworzących prostokąt, obliczenie pola jest tak proste jak podstawienie tych wartości do wzoru na pole prostokąta. Otrzymujemy więc:
Pole prostokąta = (4) × (3)
Pole prostokąta = 12 [cm²]
Obliczanie pola prostokąta na podstawie przekątnej i długości jednego z jego boków
Może się zdarzyć, że w treści zadania podana jest tylko długość przekątnej i długość jednego z boków prostokąta (bok znany). W takim przypadku możemy zastosować twierdzenie Pitagorasa, aby określić wartość brakującego boku i zastosować wzór na pole prostokąta, który został podany wcześniej.
Zastosowanie twierdzenia Pitagorasa do prostokąta
Przekątna² = (bok a)² + (bok b)²
Ponieważ w treści zadania podano długość przekątnej i długość jednego z boków, otrzymujemy następujące równanie:
Po przekształceniu „brakującego boku” w równaniu, uzyskujemy następujący związek:
Ten związek dotyczy wszystkich prostokątów i pozwoli Ci uzyskać długość boku, który musisz poznać. Po znalezieniu tej wartości, możesz bez problemu zastosować wzór na pole prostokąta, jak opisano w żółtym pudełku na początku tego artykułu.