Pole kwadratu

Czym jest kwadrat?

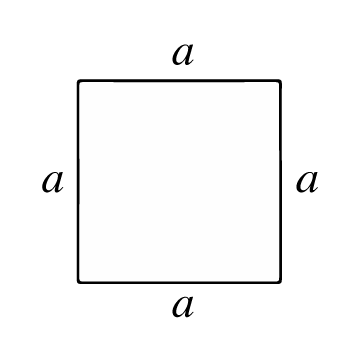
Kwadrat to wielokąt o czterech równych bokach i prostych kątach. Wszystkie jego boki są kongruentne (mają tę samą długość), a jego przekątne są również kongruentne (mają tę samą długość). Punkty przecięcia to wierzchołki, a od nich tworzą się cztery kąty wewnętrzne o kącie 90° każdy.

Jak obliczyć pole kwadratu

Pole kwadratu reprezentuje liczbę jednostek powierzchni wewnątrz kwadratu. Aby obliczyć tę powierzchnię, należy najpierw poznać długość jego boku (a), czyli długość linii łączącej dwa wierzchołki kwadratu.

Wzór na obliczenie pola kwadratu:

Przykład praktyczny

Załóżmy, że musimy obliczyć pole kwadratu, a jego bok (a) wynosi 4 [cm].

Podstawiamy wartość boku do wzoru na pole

Jeśli mamy już długość boku (4 cm), pozostaje tylko podstawić tę wartość do wzoru, aby obliczyć pole kwadratu. Otrzymujemy:

Obliczanie pola kwadratu z przekątnej

Może się zdarzyć, że w zadaniu mamy tylko długość przekątnej kwadratu. W takim przypadku można zastosować twierdzenie Pitagorasa do wyznaczenia długości boku kwadratu, zakładając, że przekątna jest przeciwprostokątną trójkąta prostokątnego o kątach 45°, 45° i 90°.

Wzór Pitagorasa

Z definicji wszystkie boki kwadratu są równej długości. Słusznie można przyjąć, że w przypadku każdego trójkąta utworzonego przez przekątną kwadratu podstawa i wysokość będą równe. Jeśli uznamy przekątną za przeciwprostokątną, możemy zapisać twierdzenie Pitagorasa w następujący sposób:

Rozwiązując równanie dla boku, uzyskujemy następujący wzór:

Ten wzór jest stosowany do wszystkich kwadratów i pozwala na wyznaczenie długości boku za pomocą dowolnego kalkulatora. Po poznaniu długości boku można podstawić go do wzoru na pole kwadratu podanego powyżej.

Jak obliczyć pole kwadratu z obwodu?

Obliczenie pola kwadratu na podstawie obwodu jest bardzo proste, ponieważ kwadrat, z definicji, ma 4 boki (a krawędzie) tej samej długości. Mając tę podstawową informację, możemy wywnioskować, że bok kwadratu jest równy obwodowi podzielonemu przez 4.

Podstawiając do wzoru na pole kwadratu, otrzymujemy:

Przykład praktyczny

Załóżmy, że musimy obliczyć pole kwadratu o obwodzie 24 [cm]. Podstawiając wartość obwodu do wzoru, otrzymujemy: