Suorakulmion pinta-ala
Syötä suorakulmion sivujen pituudet laskettaessa sen pinta-alaa. Käytä pistettä desimaalierottimena.
Suorakulmion pinta-ala on:
Mitä suorakulmio on?
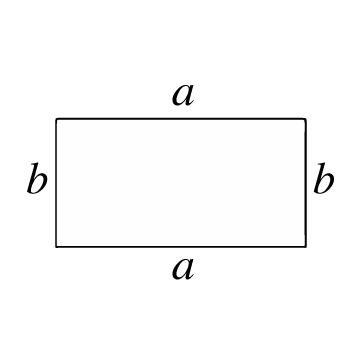
Se on suljettu monikulmio, joka koostuu 4 sivusta ja 4 kulmasta, joissa jokainen sisäinen kulma muodostaa suoran kulman (90°). Vastakkaiset sivut ovat myös paralleeleja ja yhtä pitkiä. Suorakulmio on samanlainen kuin neliö, mutta kahden parin paralleelit sivut ovat eri pituisia.
Kuinka laskea suorakulmion pinta-ala
Suorakulmion pinta-ala edustaa neliöyksiköiden määrää suorakulmion sisällä. Laskettaessa tätä pinta-alaa sinun on tiedettävä sen sivujen pituudet, eli kummankin suorakulmion kärjen yhdistävien viivojen pituudet.
Suorakulmion pinta-alan kaava
Käytännön esimerkki
Oletetaan, että meidän täytyy laskea suorakulmion pinta-ala, ja meillä on sen sivujen arvot: a = 4 [cm] ja b = 3 [cm].
Arvojen korvaaminen pinta-alan kaavassa
Jos meillä on jo suorakulmion sivujen pituudet, pinta-alan laskeminen on yhtä yksinkertaista kuin korvata nämä arvot suorakulmion pinta-alan kaavassa. Joten meillä on:
Suorakulmion pinta-ala = (4) × (3)
Suorakulmion pinta-ala = 12 [cm²]
Suorakulmion pinta-alan laskeminen sen diagonaalin ja yhden sivun pituuden perusteella
On mahdollista, että tehtävänannossa meillä on vain diagonaalin pituus ja yhden suorakulmion sivun pituus (tunnettu sivu). Tällöin voimme käyttää Pythagoraan lauseketta puuttuvan sivun arvon määrittämiseksi ja soveltaa yllä mainittua suorakulmion pinta-alan kaavaa.
Pythagoraan lausekkeiden soveltaminen suorakulmioon
Diagonaali² = (sivu a)² + (sivu b)²
Koska tehtävänannossa annetaan diagonaalin ja yhden sivun pituudet, saamme seuraavan yhtälön:
Järjestämällä "puuttuvan sivun" yhtälössä saamme seuraavan suhteen:
Tämä suhde pätee kaikkiin suorakulmioihin ja antaa sinulle sen sivun pituuden, jonka tarvitset tietää. Kun löydät tämän arvon, voit soveltaa suorakulmion pinta-alan kaavaa ilman ongelmia, kuten on mainittu tämän artikkelin alussa keltaisessa laatikossa.