Área de una Esfera

¿Qué es un Esfera?

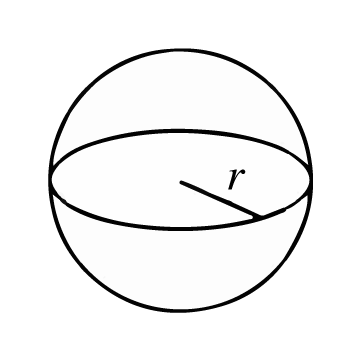
Es una figura geométrica tridimensional compuesta por una superficie curva cuyos puntos están todos a igual distancia de un punto interior denominado centro. La distancia entre la superficie curva y el centro, se denomina radio.

Cómo sacar el área de una esfera

El área de una esfera representa el número de unidades de superficie que tiene el manto o la "cáscara" de una esfera. Para calcular esta superficie, primero debes conocer cuál es la longitud de su radio (r), es decir, la distancia desde el punto central de la esfera hacia cualquier punto perteneciente al manto o superficie. Si la información que te entregan es el diámetro, puedes obtener el radio tan sólo dividiendo la longitud de su diámetro (d) en 2.

Fórmula para calcular el área de una esfera:

Área esfera = 4 · π · radio²

Ejemplo práctico

Digamos que nos piden sacar el área de una esfera y nos entregan la longitud de su diámetro, para agregarle una pequeña complejidad extra. Para este ejemplo, la longitud del diámetro tendrá un valor de 10 [cms].

Paso 1: Determinar la longitud del radio (r)

Si ya conocemos el diámetro (d) de la esfera, lo dividimos en 2 y obtenemos su radio (r). Para este ejemplo entonces, tenemos que:

Radio = diámetro ÷ 2
Radio = 10 ÷ 2 [cms]
Radio = 5 [cms]

Si en el enunciado del ejercicio, te entregan directamente el radio, entonces puedes ahorrarte este paso y continuar de inmediato al paso 2.

Paso 2: Reemplazar el radio obtenido en fórmula del área

Del paso anterior, obtuvimos el valor del radio = 5 [cms] para este ejemplo. Lo que nos queda entonces, es reemplazar esta longitud en la fórmula para calcular el área del esfera.

Área esfera = 4 · π · (5)²
Área esfera = 4 · π · 25
Área esfera = 314,16 [cms²]

Y eso es todo. De manera muy sencilla, hemos calculado el área o superficie de una esfera. Es importante recordar la relación que existe entre el diámetro y el radio, para poder resolver cualquier ejercicio matemático de este tipo.