Área de un Cuadrado

¿Qué es un cuadrado?

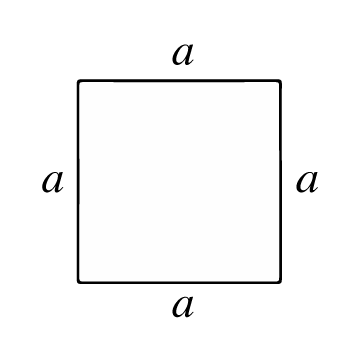
Un cuadrado es un polígono con cuatro aristas (lados) iguales y ángulos rectos. Todos sus lados son congruentes (tienen la misma longitud) y sus diagonales son congruentes (también tienen la misma longitud). Los puntos de intersección se denominan vértices y a partir de ellos, se forman 4 ángulos internos de 90º cada uno.

Cómo calcular el área de un cuadrado

El área de un cuadrado representa el número de unidades de superficie que tiene un cuadrado en su interior. Para calcular esta superfice, primero debes conocer cuál es la longitud de su lado o arista (a), es decir, el largo del trazo que une dos vértices del cuadrado.

Fórmula para calcular el área de un cuadrado:

Área cuadrado = arista²

Ejemplo práctico

Supongamos que nos piden sacar el área de un cuadrado y nos entregan el valor de su arista (a) que para este ejemplo será de 4 [cms].

Reemplazando el valor de la arista en la fórmula del área

Si ya tenemos calculado el largo de la arista (4 cms), solo nos queda entonces reemplazar este valor en la fórmula para calcular el área del cuadrado. En efecto:

Área cuadrado = arista²
Área cuadrado = (4)²
Área cuadrado = 16 [cms²]

Sacar el área de un cuadrado a partir de su diagonal

Es posible que en el enunciado de un problema, el único dato que tengas sea el largo o longitud de la diagonal de un cuadrado. En estos casos, puedes utilizar el Teorema de Pitágoras para determinar el valor de la arista del cuadrado si es que consideras que la diagonal es la Diagonal de un triángulo isóceles con ángulos interiores de 45°, 45° y 90° respectivamente.

Fórmula del Teorema de Pitágoras

Hipotenusa² = base² + altura²

Por definición, todos los lados o aristas de un cuadrado son iguales. Es válido asumir entonces que para todo triángulo formado por la diagonal de un cuadrado, la base y la altura serán iguales. Si consideramos a la diagonal como la hipotenusa, podemos reescribir la Fórmula de Pitágoras de la siguiente forma:

Diagonal² = arista² + arista²
Diagonal² = 2 · arista²
Diagonal = √2 · arista

Despejando la arista en la ecuación, nos queda la siguiente relación:

Arista = Diagonal ÷ √2

Esta relación se cumple para todos los cuadrados y te permitirá obtener el largo de la arista de manera simple utilizando cualquier calculadora. Una vez que ya conoces el valor de la arista, puedes reemplazarlo en la fórmula para sacar el área del cuadrado que mencionamos en el recuadro amarillo más arriba.

Cómo calcular el área de un cuadrado a partir de su perímetro

Calcular el área de un cuadrado a partir de su perímetro es muy sencillo, dado que por definición, un cuadrado tiene 4 aristas (a lados) del mismo tamaño. Teniendo este antecedente, podemos deducir entonces que la arista de un cuadrado es equivalente a su perímetro dividido en 4.

Reemplazando en la fórmula del área del cuadrado, tenemos:

Área cuadrado = arista²
Área cuadrado = (perímetro ÷ 4)²

Ejemplo práctico

Supongamos que nos piden sacar el área de un cuadrado que tiene un perímetro de 24 [cms]. Reemplazando el valor del perímetro en la fórmula del área tenemos:

Área cuadrado = arista²
Área cuadrado = (perímetro ÷ 4)²
Área cuadrado = (24 ÷ 4)²
Área cuadrado = (6)² = 36 [cms²]