Rektangelns yta
Skriv in längderna på sidorna på rektangeln för att beräkna dess yta. Använd punkt som decimaltecken.
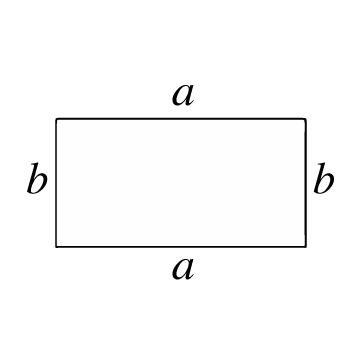
Rektangelns yta är:
Vad är en rektangel?
Det är en sluten polygon som består av 4 sidor och 4 hörn, där varje inre vinkel är en rät vinkel (90°). De motsatta sidorna är också parallella och lika långa. En rektangel är lik en kvadrat, förutom att de två paren parallella sidor har olika längder.
Hur man beräknar en rektangels yta
Rektangelns yta representerar antalet kvadratenheter inuti rektangeln. För att beräkna denna yta måste du känna till längderna på sidorna, det vill säga längden på varje linje som binder samman två hörn av rektangeln.
Formel för att beräkna rektangelns yta
Praktiskt exempel
Låt oss säga att vi måste beräkna ytan på en rektangel och vi har värdena på sidorna, där a = 4 [cm] och b = 3 [cm].
Ersätt värdena på sidorna i ytvärderingsformeln
Om vi redan har längderna på sidorna som gör rektangeln, är det lika enkelt att beräkna ytan som att ersätta dessa värden i rektangelns ytvärderingsformel. Vi får då:
Rektangelns yta = (4) × (3)
Rektangelns yta = 12 [cm²]
Beräkning av rektangelns yta baserat på dess diagonal och längden på en sida
Det är möjligt att i en uppgift ge oss endast längden på diagonalen och längden på en sida av rektangeln (den kända sidan). I detta fall kan vi använda Pythagoras sats för att bestämma värdet på den saknade sidan och använda den tidigare nämnda formeln för rektangelns yta.
Pythagoras sats applicerad på en rektangel
Diagonal² = (sida a)² + (sida b)²
Eftersom uppgiften ger oss diagonalen och en av sidlängderna, får vi följande ekvation:
Genom att omvandla den "saknade sidan" i ekvationen får vi följande relation:
Denna relation gäller för alla rektanglar och kommer att låta dig hitta den sida som du behöver veta. När du hittar detta värde kan du enkelt tillämpa formeln för rektangelns yta utan problem, som nämnts i den gula rutan i början av denna artikel.