Área da Esfera

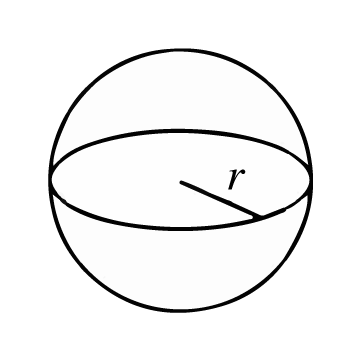
O Que É uma Esfera?

É uma figura geométrica tridimensional composta por uma superfície curva cujos pontos estão todos a igual distância de um ponto interior chamado centro. A distância entre a superfície curva e o centro é chamada raio.

Como Calcular a Área de uma Esfera

A área de uma esfera representa o número de unidades de superfície na casca ou "pele" de uma esfera. Para calcular essa superfície, você precisa saber o comprimento do raio (r), que é a distância do ponto central da esfera a qualquer ponto na superfície. Se você tiver o diâmetro, pode obter o raio simplesmente dividindo o comprimento do diâmetro (d) por 2.

Fórmula para Calcular a Área de uma Esfera:

Área da Esfera = 4 * π * raio²

Exemplo Prático

Vamos supor que precisamos encontrar a área de uma esfera e nos é fornecido o diâmetro, adicionando um pouco mais de complexidade. Para este exemplo, o comprimento do diâmetro é de 10 [cm].

Passo 1: Determinar o Comprimento do Raio (r)

Se já sabemos o diâmetro (d) da esfera, dividimos por 2 para obter o raio (r). Para este exemplo, temos:

Raio = Diâmetro ÷ 2
Raio = 10 ÷ 2 [cm]
Raio = 5 [cm]

Se o enunciado do exercício fornecer o raio diretamente, você pode pular esta etapa e prosseguir diretamente para a etapa 2.

Passo 2: Substituir o Raio Obtido na Fórmula da Área

Da etapa anterior, obtivemos o valor do raio = 5 [cm] para este exemplo. O que resta é substituir esse comprimento na fórmula para calcular a área da esfera.

Área da Esfera = 4 * π * (5)²
Área da Esfera = 4 * π * 25
Área da Esfera = 314,16 [cm²]

E é isso. Calculamos a área ou superfície de uma esfera de maneira muito simples. É importante lembrar a relação entre diâmetro e raio para resolver quaisquer exercícios matemáticos desse tipo.