Flächeninhalt eines Rechtecks
Geben Sie die Länge der Seiten des Rechtecks ein, um seine Fläche zu berechnen. Verwenden Sie den Punkt als Dezimaltrennzeichen.
Die Fläche des Rechtecks beträgt:
Was ist ein Rechteck?
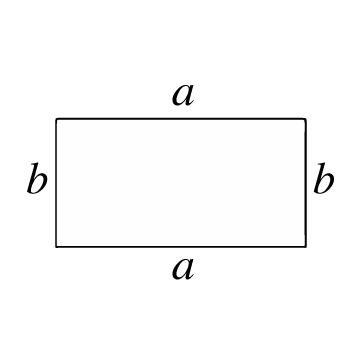
Es ist ein geschlossenes Polygon, das aus 4 Seiten und 4 Ecken besteht, wobei jeder Innenwinkel einen rechten Winkel (90°) bildet. Die gegenüberliegenden Seiten sind auch parallel und haben die gleiche Länge. Ein Rechteck ähnelt einem Quadrat, außer dass die 2 Paare paralleler Seiten unterschiedliche Längen haben.
Wie berechnet man die Fläche eines Rechtecks?
Die Fläche eines Rechtecks repräsentiert die Anzahl der Quadratflächeneinheiten, die ein Rechteck im Inneren hat. Um diese Fläche zu berechnen, müssen Sie zuerst die Länge seiner Seiten kennen, das heißt, die Länge jedes Strichs, der zwei Ecken des Rechtecks verbindet.
Formel zur Berechnung der Fläche eines Rechtecks
Praktisches Beispiel
Angenommen, Sie werden gebeten, den Flächeninhalt eines Rechtecks zu berechnen, und Ihnen werden die Werte seiner Seiten gegeben, wobei a = 4 [cm] und b = 3 [cm] ist.
Ersetzen der Werte der Seiten in die Flächenberechnungsformel
Wenn Sie bereits die Länge der Seiten, die das Rechteck bilden, haben, müssen Sie diese Werte nur noch in die Formel für die Berechnung der Fläche des Rechtecks einsetzen. Auf diese Weise haben wir:
Flächeninhalt Rechteck = (4) · (3)
Flächeninhalt Rechteck = 12 [cm²]
Berechnen der Fläche eines Rechtecks anhand seiner Diagonale und der Länge einer seiner Seiten
Es kann vorkommen, dass Sie in der Aufgabenstellung nur die Länge der Diagonalen und die Länge einer seiner Seiten des Rechtecks (bekannte Seite) gegeben werden. In solchen Fällen können Sie den Satz des Pythagoras verwenden, um die Länge der Seite zu berechnen, die Ihnen noch fehlt (fehlende Seite), und die oben erwähnte Formel zur Berechnung der Fläche des Rechtecks anwenden.
Satz des Pythagoras auf ein Rechteck angewandt
Diagonale² = (Seite a)² + (Seite b)²
Da in der Aufgabenstellung die Länge der Diagonale und die Länge einer seiner Seiten gegeben sind, können wir die folgende Gleichung verwenden:
Indem wir die fehlende Seite in der Gleichung isolieren, erhalten wir folgende Beziehung:
Diese Beziehung gilt für alle Rechtecke und ermöglicht es Ihnen, die Länge der Seite zu berechnen, die Sie noch nicht kennen. Sobald Sie diesen Wert gefunden haben, können Sie problemlos die oben genannte Formel zur Berechnung der Fläche des Rechtecks anwenden.