Area di una Sfera
Inserisci la lunghezza del raggio nella formula per calcolare l'area o superficie di una sfera. Utilizza il punto come separatore decimale.
L'area della sfera è:
Cos'è una Sfera?
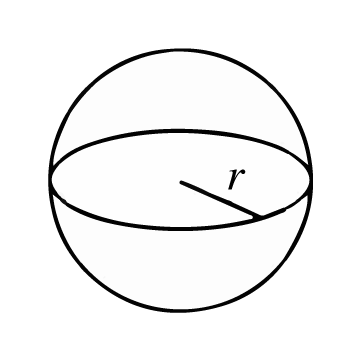
È una figura geometrica tridimensionale composta da una superficie curva i cui punti sono tutti a uguale distanza da un punto interno denominato centro. La distanza tra la superficie curva e il centro è chiamata raggio.
Come calcolare l'area di una sfera
L'area di una sfera rappresenta il numero di unità di superficie che ha il manto o la "corteccia" di una sfera. Per calcolare questa superficie, devi prima conoscere la lunghezza del suo raggio (r), cioè la distanza dal punto centrale della sfera a qualsiasi punto appartenente al manto o superficie. Se le informazioni fornite sono il diametro, puoi ottenere il raggio semplicemente dividendo la lunghezza del diametro (d) per 2.
Formula per calcolare l'area di una sfera:
Esempio pratico
Supponiamo che ci venga chiesto di calcolare l'area di una sfera e ci venga fornita la lunghezza del suo diametro, per aggiungere un po' di complessità. Per questo esempio, la lunghezza del diametro sarà di 10 [cm].
Passo 1: Determinare la lunghezza del raggio (r)
Se conosciamo già il diametro (d) della sfera, lo dividiamo per 2 e otteniamo il suo raggio (r). Per questo esempio quindi, abbiamo che:
Raggio = 10 ÷ 2 [cm]
Raggio = 5 [cm]
Se nell'enunciato dell'esercizio ti danno direttamente il raggio, puoi saltare questo passo e passare direttamente al passo 2.
Passo 2: Sostituire il raggio ottenuto nella formula dell'area
Dal passo precedente, abbiamo ottenuto il valore del raggio = 5 [cm] per questo esempio. Quello che ci resta da fare è sostituire questa lunghezza nella formula per calcolare l'area della sfera.
Area sfera = 4 · π · 25
Area sfera = 314,16 [cm²]
E questo è tutto. In modo molto semplice, abbiamo calcolato l'area o superficie di una sfera. È importante ricordare la relazione esistente tra diametro e raggio, per poter risolvere qualsiasi esercizio matematico di questo tipo.