Area di un Quadrato

Cos'è un quadrato?

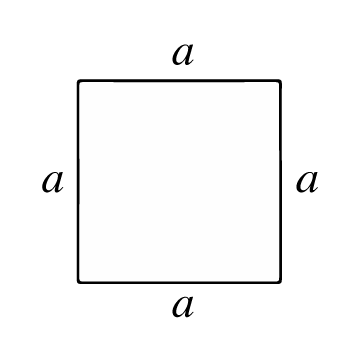
Un quadrato è un poligono con quattro lati (lati) uguali e angoli retti. Tutti i suoi lati sono congruenti (hanno la stessa lunghezza) e le sue diagonali sono congruenti (anch'esse hanno la stessa lunghezza). I punti di intersezione si chiamano vertici e da essi si formano 4 angoli interni di 90° ciascuno.

Come calcolare l'area di un quadrato

L'area di un quadrato rappresenta il numero di unità di superficie che ha un quadrato al suo interno. Per calcolare questa superficie, prima devi conoscere la lunghezza del suo lato o arista (a), cioè la lunghezza della linea che unisce due vertici del quadrato.

Formula per calcolare l'area di un quadrato:

Esempio pratico

Supponiamo che ci venga chiesto di calcolare l'area di un quadrato e ci venga fornito il valore del suo lato (a) che per questo esempio sarà di 4 [cm].

Sostituendo il valore del lato nella formula dell'area

Se abbiamo già calcolato la lunghezza del lato (4 cm), ci rimane solo da sostituire questo valore nella formula per calcolare l'area del quadrato. Infatti:

Calcolare l'area di un quadrato a partire dalla sua diagonale

È possibile che nel testo di un problema, l'unico dato che hai sia la lunghezza o il valore della diagonale di un quadrato. In questi casi, puoi utilizzare il Teorema di Pitagora per determinare il valore del lato del quadrato, considerando che la diagonale forma un triangolo isoscele con angoli interni di 45°, 45° e 90° rispettivamente.

Formula del Teorema di Pitagora

Per definizione, tutti i lati o ariste di un quadrato sono uguali. È valido assumere quindi che per ogni triangolo formato dalla diagonale di un quadrato, la base e l'altezza saranno uguali. Se consideriamo la diagonale come l'ipotenusa, possiamo riscrivere la formula di Pitagora nel seguente modo:

Isolando il lato nell'equazione, otteniamo la seguente relazione:

Questa relazione è valida per tutti i quadrati e ti permetterà di ottenere la lunghezza del lato in modo semplice utilizzando qualsiasi calcolatrice. Una volta conosciuto il valore del lato, puoi sostituirlo nella formula per calcolare l'area del quadrato menzionata nel riquadro giallo qui sopra.

Come calcolare l'area di un quadrato a partire dal suo perimetro

Calcolare l'area di un quadrato a partire dal suo perimetro è molto semplice, dato che per definizione, un quadrato ha 4 lati (lati) della stessa dimensione. Avendo questa premessa, possiamo dedurre che il lato di un quadrato è equivalente al suo perimetro diviso per 4.

Sostituendo nella formula dell'area del quadrato, abbiamo:

Esempio pratico

Supponiamo che ci venga chiesto di calcolare l'area di un quadrato che ha un perimetro di 24 [cm]. Sostituendo il valore del perimetro nella formula dell'area otteniamo: