আয়তক্ষেত্রের ক্ষেত্রফল
আয়তক্ষেত্রের ক্ষেত্রফল বা পৃষ্ঠতল গণনা করতে বাহুগুলির দৈর্ঘ্য লিখুন। দশমিক বিভাজক হিসেবে বিন্দু ব্যবহার করুন।
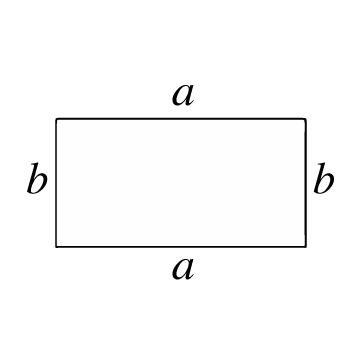
আয়তক্ষেত্রের ক্ষেত্রফল হলো:
আয়তক্ষেত্র কী?
এটি 4টি বাহু এবং 4টি শীর্ষবিন্দু দ্বারা গঠিত একটি বদ্ধ বহুভুজ, যেখানে প্রতিটি অন্তঃকোণ একটি সমকোণ (90°) তৈরি করে। বিপরীত বাহুগুলি সমান্তরাল এবং একই দৈর্ঘ্যের। একটি আয়তক্ষেত্র একটি বর্গক্ষেত্রের মতো, তবে পার্থক্য হলো 2 জোড়া সমান্তরাল বাহুর দৈর্ঘ্য ভিন্ন।
আয়তক্ষেত্রের ক্ষেত্রফল কীভাবে গণনা করবেন
আয়তক্ষেত্রের ক্ষেত্রফল হলো আয়তক্ষেত্রের অভ্যন্তরে থাকা পৃষ্ঠতলের একক সংখ্যা। এই পৃষ্ঠতল গণনা করতে, প্রথমে আপনাকে এর বাহুগুলির দৈর্ঘ্য জানতে হবে, অর্থাৎ আয়তক্ষেত্রের দুটি শীর্ষবিন্দু যুক্তকারী প্রতিটি রেখার দৈর্ঘ্য।
আয়তক্ষেত্রের ক্ষেত্রফল গণনার সূত্র
ব্যবহারিক উদাহরণ
ধরা যাক আমাদের একটি আয়তক্ষেত্রের ক্ষেত্রফল বের করতে বলা হয়েছে এবং আমাদের এর বাহুগুলির মান দেওয়া হয়েছে, a = 4 [সেমি] এবং b = 3 [সেমি]।
ক্ষেত্রফলের সূত্রে বাহুগুলির মান প্রতিস্থাপন
যদি আমরা ইতিমধ্যে আয়তক্ষেত্র গঠনকারী বাহুগুলির দৈর্ঘ্য জানি, তাহলে ক্ষেত্রফল গণনা করতে শুধু এই মানগুলি আয়তক্ষেত্রের ক্ষেত্রফলের সূত্রে প্রতিস্থাপন করতে হবে। এইভাবে:
আয়তক্ষেত্রের ক্ষেত্রফল = (4) · (3)
আয়তক্ষেত্রের ক্ষেত্রফল = 12 [সেমি²]
কর্ণ এবং একটি বাহুর দৈর্ঘ্য থেকে আয়তক্ষেত্রের ক্ষেত্রফল বের করা
এটা সম্ভব যে কোনো সমস্যার বিবরণে আমাদের শুধু কর্ণের দৈর্ঘ্য এবং আয়তক্ষেত্রের একটি বাহুর (জানা বাহু) দৈর্ঘ্য দেওয়া হয়। এই ক্ষেত্রে, আমরা পিথাগোরাসের উপপাদ্য ব্যবহার করে অজানা বাহুর মান নির্ধারণ করতে পারি এবং উপরে উল্লিখিত আয়তক্ষেত্রের ক্ষেত্রফলের সূত্র প্রয়োগ করতে পারি।
আয়তক্ষেত্রে প্রয়োগকৃত পিথাগোরাসের উপপাদ্যের সূত্র
কর্ণ² = (বাহু a)² + (বাহু b)²
যেহেতু সমস্যার বিবরণে আমাদের কর্ণের দৈর্ঘ্য এবং একটি বাহুর দৈর্ঘ্য দেওয়া হয়েছে, আমরা নিম্নলিখিত সমীকরণ পেতে পারি:
সমীকরণ থেকে "অজানা বাহু" নিষ্কাশন করলে, নিম্নলিখিত সম্পর্ক পাওয়া যায়:
এই সম্পর্ক সকল আয়তক্ষেত্রের জন্য প্রযোজ্য এবং এটি আপনাকে অজানা বাহুর দৈর্ঘ্য বের করতে সাহায্য করবে। এই মান পাওয়ার পর, আপনি এই নিবন্ধের শুরুতে হলুদ বাক্সে উল্লিখিত আয়তক্ষেত্রের ক্ষেত্রফলের সূত্র সমস্যা ছাড়াই প্রয়োগ করতে পারেন।