गोले का क्षेत्रफल

गोला क्या है?

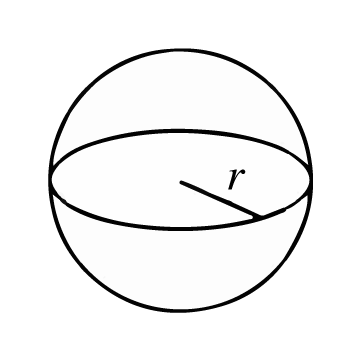
यह एक त्रिआयामी ज्यामितीय आकृति है जो एक वक्र सतह से बनी होती है जिसके सभी बिंदु एक आंतरिक बिंदु से समान दूरी पर होते हैं जिसे केंद्र कहा जाता है। वक्र सतह और केंद्र के बीच की दूरी को त्रिज्या कहा जाता है।

गोले का क्षेत्रफल कैसे निकालें

गोले का क्षेत्रफल उसके आवरण या "छिलके" में सतह इकाइयों की संख्या को दर्शाता है। इस सतह की गणना करने के लिए, पहले आपको इसकी त्रिज्या (r) की लंबाई जानना आवश्यक है, अर्थात गोले के केंद्रीय बिंदु से आवरण या सतह पर किसी भी बिंदु तक की दूरी। यदि आपको व्यास की जानकारी दी गई है, तो आप उसके व्यास (d) की लंबाई को 2 से भाग देकर त्रिज्या प्राप्त कर सकते हैं।

गोले का क्षेत्रफल गणना करने का सूत्र:

व्यावहारिक उदाहरण

मान लीजिए कि हमसे एक गोले का क्षेत्रफल निकालने को कहा गया है और हमें उसके व्यास की लंबाई दी गई है, थोड़ी अतिरिक्त जटिलता जोड़ने के लिए। इस उदाहरण के लिए, व्यास की लंबाई 10 [सेमी] होगी।

चरण 1: त्रिज्या (r) की लंबाई निर्धारित करें

यदि हम पहले से गोले का व्यास (d) जानते हैं, तो इसे 2 से भाग देने पर हमें इसकी त्रिज्या (r) प्राप्त होती है। इस उदाहरण के लिए:

यदि प्रश्न में आपको सीधे त्रिज्या दी गई है, तो आप इस चरण को छोड़ सकते हैं और तुरंत चरण 2 पर जा सकते हैं।

चरण 2: प्राप्त त्रिज्या को क्षेत्रफल के सूत्र में प्रतिस्थापित करें

पिछले चरण से, इस उदाहरण के लिए हमें त्रिज्या = 5 [सेमी] का मान प्राप्त हुआ। अब हमें बस इस लंबाई को गोले के क्षेत्रफल की गणना के सूत्र में प्रतिस्थापित करना है।

बस इतना ही। बहुत सरल तरीके से, हमने एक गोले के क्षेत्रफल या सतह की गणना कर ली है। इस प्रकार के किसी भी गणितीय अभ्यास को हल करने के लिए व्यास और त्रिज्या के बीच के संबंध को याद रखना महत्वपूर्ण है।