Rectangle Area
Enter the length of the sides of the rectangle to calculate its area. Use a period as the decimal separator.
The area of the rectangle is:
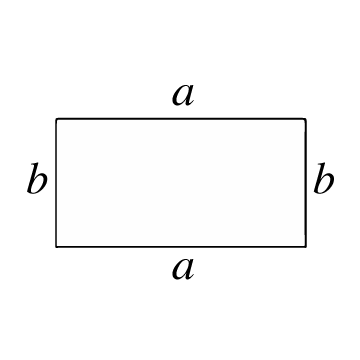
What is a Rectangle?
It is a closed polygon formed by 4 sides and 4 vertices, where each interior angle forms a right angle (90°). The opposite sides are also parallel and of the same length. A rectangle is similar to a square, except that the 2 pairs of parallel sides have different lengths.
How to Calculate the Area of a Rectangle
The area of a rectangle represents the number of square units inside a rectangle. To calculate this area, you need to know the length of its sides, i.e., the length of each line connecting two vertices of the rectangle.
Formula to Calculate the Area of a Rectangle
Practical Example
Let's say we need to calculate the area of a rectangle, and we are given the values of its sides, with a = 4 [cms] and b = 3 [cms].
Replacing the values of its sides in the area formula
If we already have the lengths of the sides that make up the rectangle, calculating the area is as simple as replacing these values in the rectangle area formula. Thus, we have:
Rectangle Area = (4) × (3)
Rectangle Area = 12 [cms²]
Calculating the area of a rectangle based on its diagonal and the length of one of its sides
It is possible that in a problem statement, we are given only the length of the diagonal and the length of one of the sides of the rectangle (the known side). In these cases, we can use the Pythagorean Theorem to determine the value of the missing side (the missing side) and apply the rectangle area formula mentioned above.
Pythagorean Theorem formula applied to a rectangle
Diagonal² = (side a)² + (side b)²
Since the exercise statement gives us the length of the diagonal and the length of one of its sides, we can obtain the following equation:
By rearranging the "missing side" in the equation, we have the following relationship:
This relationship applies to all rectangles and will allow you to obtain the length of the side that you need to know. Once you find this value, you can apply the rectangle area formula without any problems as mentioned in the yellow box at the beginning of this article.