Cube Area
Enter the length of the edge to calculate the area or surface of a cube. Use a period as the decimal separator.
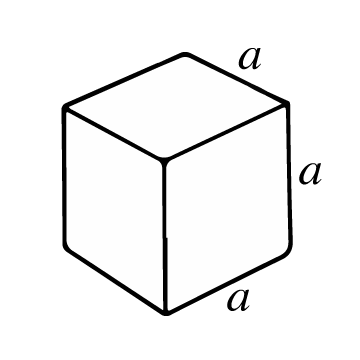
The area of the cube is:
What is a Cube?
It is a three-dimensional geometric figure formed by six congruent square faces. A cube is created by the union of 8 equidistant vertices, using 12 edges of equal length, which form right angles with their adjacent ones.
How to Calculate the Area of a Cube?
The area of a cube represents the total number of square surface units occupied by the six faces of the cube as a whole.
By definition, we know that a cube is formed by six congruent square faces. If we know the area of one face, we can obtain the total area of the cube by summing the surface area of each face. In other words, the area of the square multiplied by 6.
Formula to Calculate the Area of a Cube:
First, obtain the area of one of its faces in the same way you would with a square. Then, to get the total area, simply multiply the area of one face by 6 in mathematical terms.
Practical Example
Let's say we need to find the area of a cube, and we are given the value of its edge (a), which, for this example, is 4 [cm].
Replacing the value of the edge in the area formula
We already have the length of the edge (4 cm). To calculate the area of the cube, simply replace the value of the edge in the formula:
Cube Area = 6 · (4)²
Cube Area = 6 · 16
Cube Area = 96 [cm²]